サブスクサービスでよく見られる J カーブを、いくつかの仮定から定式化して、その振る舞いをいくつか見ていく。
最後には、素朴な直感に反する面白い結果も得られる。
定式化#
$c$ を CAC, つまり一人の顧客を獲得するのにかかるコスト、 $r$ を一人の顧客を獲得したときの粗利、つまり収益から原価を取り除いたものとする。
このとき、一人の顧客を獲得したときの利益は、
$$ r - c. $$
さて、毎月 $M$ 人の顧客を獲得すると仮定する。このとき、起点となる月から $N$ ヶ月目までの累積利益 $R(N)$ は、
$$ \begin{aligned} R(N) &= (Mr-Mc) + (2Mr-Mc) + (3Mr-Mc) + \cdots + (NMr-Mc) \\ &= Mr \sum_{n=1}^{N} n - M \sum_{n=1}^{N} c \\ &= Mr \left( \frac{N(N+1)}{2} \right) - McN \\ &= \frac{Mr}{2} N^2 + M \left( \frac{r}{2} - c \right)N. \end{aligned} $$
これは $N$ に関する二次関数。
粗利 1,000 円、 CAC 10,000 円のサービスで、36 ヶ月間毎月 10 人ずつ獲得したとすると、そのグラフは以下のようになる:
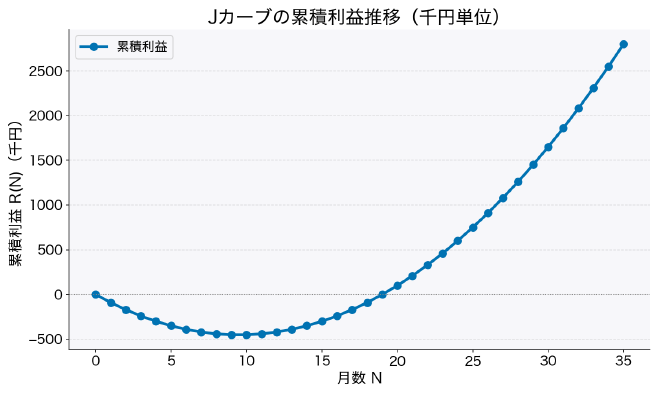
損益分岐点 $N_p (> 0)$ を求めよう。 $R(N_p) = 0$ となる $N_p$ を求めればよい。
$$ \begin{aligned} \frac{Mr}{2} N_p^2 + M \left( \frac{r}{2} - c \right)N_p &= 0 \\ \frac{r}{2} N_p + \frac{r}{2} -c&= 0 \\ N_p &= \frac{2c}{r} - 1. \end{aligned} $$
さて、いくつか見ていく。
「粗利 > CAC ならば、 J カーブは起きない」#
そらそうやろと思うが、上の式からも言える。
$N$ が自然数であることに注意する。 J カーブが起きない、というのは $N \geq 1$ のとき $R(N) \geq 0$ ということである。
これはすなわち、 $R(N)$ と横軸の 2 つの交点の右側 $N_p$ が $N_p \leq 1$ であることを意味する。すなわち以下が成立する:
$$ \frac{2c}{r} - 1 \leq 1, $$
すなわち、
$$ c \leq r. $$
「損益分岐点は、一ヶ月に顧客を何人獲得しようが変わらない」#
ここからは $c > r$ と仮定しよう。
この主張はなかなか面白い。素朴にたくさん顧客を獲得すれば、それだけ損益分岐点は早く来るように思う。
しかし、それは $N_p = \frac{2c}{r} - 1$ を眺めてみると否定できる。 $N_p$ は $M$ に依存していない。すなわち、損益分岐点は月ごとの顧客獲得数に依存しない。
実際、 M の値をいくつか変えたグラフを重ねてみる。すべて同じ点を通る:
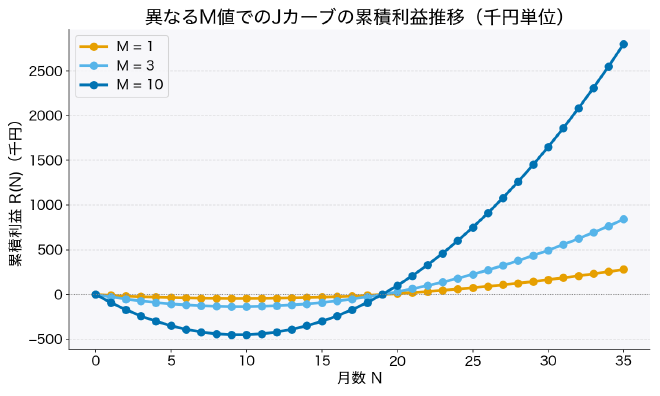
ついでに、 ROI の逆数 $I = \frac{c}{r}$ が不変であれば、 $N_p$ は $I$ に依存しないことがわかる。
「損益分岐点以降の利益は何に依存するか」#
$R(N)$ の傾きをみてみる。これを連続関数と見立てて微分してみると
$$ \begin{aligned} R’(N) &= MrN + M \left( \frac{r}{2} - c \right) \\ \end{aligned}. $$
特に $N$ の係数に注目すると、粗利と獲得顧客数に依存している ことがわかる。 CAC は対してカーブの角度には寄与しない こともわかる。
「カーブの落ち込み具合は何に依存するか?」#
カーブの落ち込み具合の振る舞いをみてみる。上のグラフから、少なくとも $M$ に依存していることが見て取れるが。
カーブの最小値を出してみよう。
$R(N)$ が最小となる点 $N_{min}$ は、横軸との交点が $0$ と $N_p$ とわかっているから、その中点 $N_{min} = \frac{N_p}{2}$ である。
$R(N_{min})$ は、
$$ \begin{aligned} R(N_{min}) &= \frac{Mr}{2} \left( \frac{N_p}{2} \right)^2 + M \left( \frac{r}{2} - c \right) \frac{N_p}{2} \\ &= \frac{Mr}{2}\left[\frac12\left(\frac{2c}{r}-1\right)\right]^{2} + M\left(\frac{r}{2}-c\right)\frac12\left(\frac{2c}{r}-1\right) \\ &= \frac{Mr}{2}\left(\frac{c}{r}-\frac12\right)^{2} + M\left(c-\frac{r}{4}-\frac{c^{2}}{r}\right) \\ &= \frac{M}{2}\left(\frac{c^{2}}{r}-c+\frac{r}{4}\right)+ M\left(c-\frac{r}{4}-\frac{c^{2}}{r}\right) \\ &= -\frac{M c^{2}}{2r} + \frac{M c}{2} - \frac{M r}{8} \\ &= \frac{M}{8r}\left(-4c^{2}+4cr-r^{2}\right) \\ &= -\frac{M}{8r} \bigl(2c-r\bigr)^{2}. \end{aligned} $$
ここから、 $M$, すなわち顧客獲得数がが大きいほど、 J の落ち込みは深くなる ことがわかる。
また、 $c$ と $r$ のオーダーをそれぞれ見てみると、
- $c$ については $O(c^2)$
- $r$ については $O(r)$
となっている。これはすなわち、 CAC を 1/10 倍にするのと、粗利を 10 倍にするのでは、 CAC の減少の効果のほうがはるかに大きい ことを意味する。これはなかなか示唆的である。
さらに、 ROI の逆数 $I = \frac{c}{r}$ で整理すると、
$$ R(N_{min}) = -\frac{rM}{8} \left( 2I - 1 \right)^2. $$
となる。つまり、 費用対効果の比が不変であれば、粗利の絶対量が大きいほど J の落ち込みは深くなる ことがわかる。 ROI の比だけが重要ではないのだ。ちゃんと量も稼がないといけない。
これもなかなかおもしろい。グラフにしてみても確かにそうみたいだ:
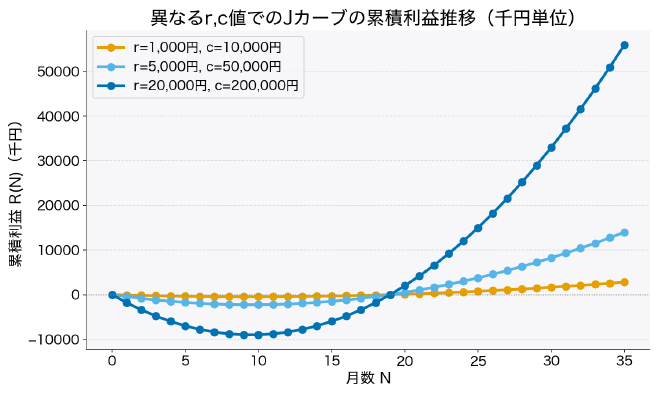
(ちなみに損益分岐点は $I$ が不変なので、全部同じ)
おわり

